En Breve (TL;DR)
El enfoque ingenieril transforma los KPI en señales a procesar, permitiendo separar nítidamente la información estratégica del ruido de fondo de los datos.
El análisis en el dominio de la frecuencia con la Transformada de Fourier revela ciclicidades invisibles, superando las intuiciones basadas en la simple observación temporal.
Implementar el filtro de Kalman ofrece una estimación de la tendencia en tiempo real, eliminando el retraso en la toma de decisiones causado por las clásicas medias móviles.
El diablo está en los detalles. 👇 Sigue leyendo para descubrir los pasos críticos y los consejos prácticos para no equivocarte.
En el panorama de la Business Intelligence moderna, el análisis de series temporales representa a menudo la frontera entre una decisión basada en la intuición y una fundada en la ciencia de datos. Sin embargo, la mayoría de los analistas se limita a observar medias móviles y variaciones porcentuales, ignorando un patrimonio metodológico que la ingeniería electrónica ha perfeccionado en las últimas décadas: el Signal Processing (Procesamiento Digital de Señales).
En esta guía técnica, abandonaremos el enfoque estadístico clásico para adoptar una visión ingenieril. Trataremos los KPI empresariales (como el volumen de solicitudes de hipotecas en una Fintech o el flujo de caja diario) no como simples números en una hoja de cálculo, sino como señales eléctricas afectadas por ruido. Aplicando transformadas matemáticas y filtros digitales, aprenderemos a extraer la “tendencia pura” (la señal) de las fluctuaciones aleatorias del mercado (el ruido).

1. La Mentalidad Ingenieril: Señal vs Ruido
En electrónica, una señal recibida por un sensor siempre está contaminada por perturbaciones externas. Lo mismo ocurre con los datos empresariales. Si observamos el gráfico de las ventas diarias, vemos picos y valles. La pregunta fundamental es: ¿esa caída del martes es una tendencia preocupante (Señal) o solo una variación aleatoria debida al clima o a un día festivo (Ruido)?
Para responder, debemos definir la relación Señal/Ruido (SNR – Signal-to-Noise Ratio). Un enfoque basado en la física de sistemas nos enseña que:
- La Señal es la información determinista, a menudo de baja frecuencia (tendencia de crecimiento) o con frecuencia específica (estacionalidad).
- El Ruido es estocástico, a menudo de alta frecuencia y distribuido aleatoriamente (ruido blanco gaussiano).
2. Herramientas y Prerrequisitos
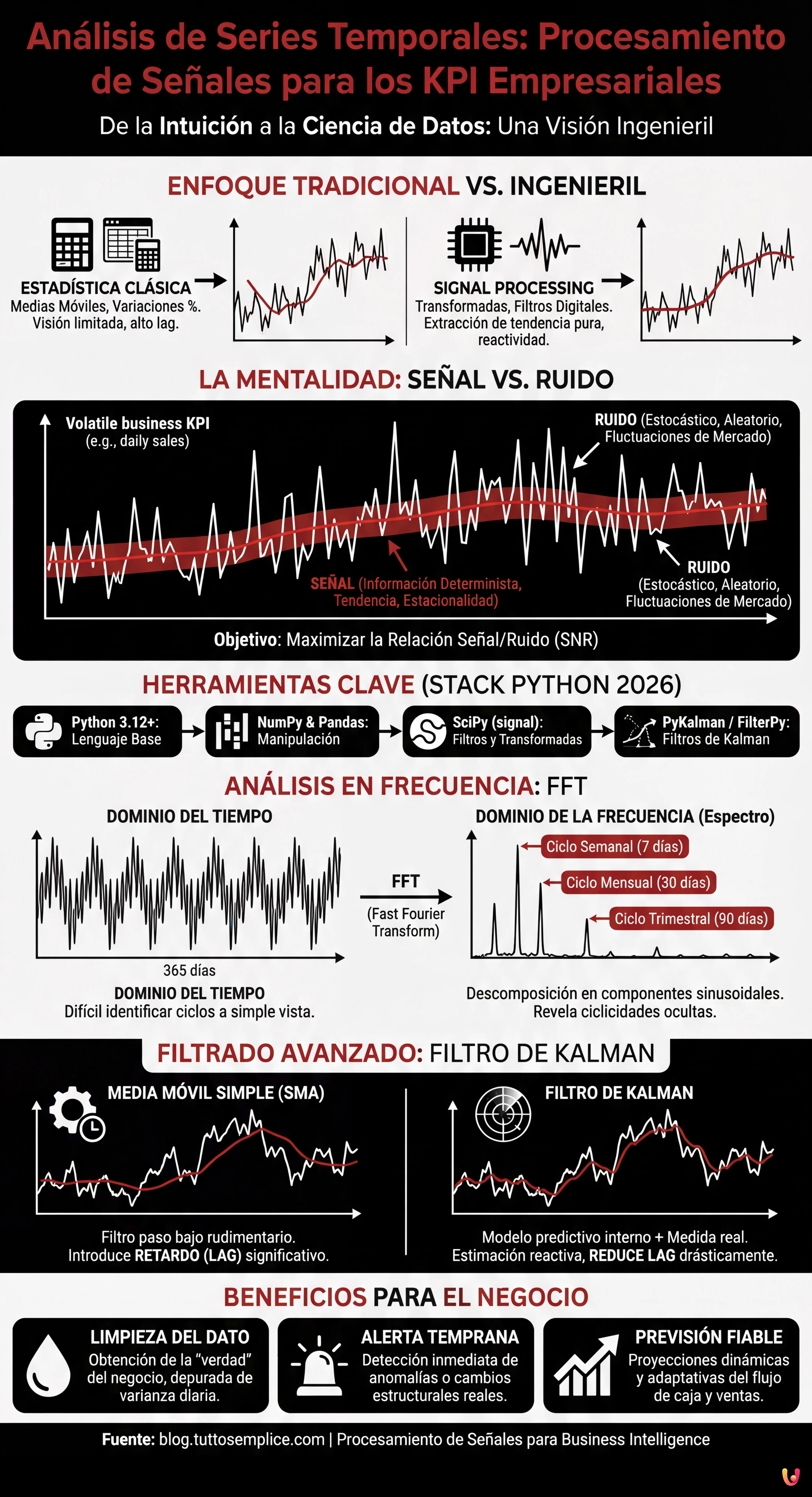
Para seguir esta guía, no usaremos Excel. El análisis avanzado de señales requiere potencia de cálculo y librerías específicas. En 2026, el stack estándar para este tipo de operación incluye:
- Python 3.12+: El lenguaje de referencia.
- NumPy & Pandas: Para la manipulación de las series temporales.
- SciPy (módulo signal): Para la implementación de filtros digitales y transformadas.
- PyKalman o FilterPy: Librerías optimizadas para la implementación de los filtros de Kalman.
3. Análisis en el Dominio de la Frecuencia: La Transformada de Fourier (FFT)

Uno de los errores más comunes en el análisis de series temporales financieras es intentar intuir la estacionalidad mirando el gráfico en el dominio del tiempo. Un ingeniero electrónico, en cambio, traslada el problema al dominio de la frecuencia.
Utilizando la Fast Fourier Transform (FFT), podemos descomponer nuestro KPI (ej. solicitudes de hipotecas diarias) en sus componentes sinusoidales constitutivos. Esto nos permite identificar ciclicidades ocultas que el ojo humano no ve.
Aplicación Práctica: Detectar la Ciclicidad de las Hipotecas
Imaginemos que tenemos un dataset de 365 días de solicitudes. Aplicando la FFT, podríamos ver un pico de magnitud en la frecuencia correspondiente a 7 días (ciclo semanal) y uno a 30 días (ciclo mensual). Si notamos un pico inesperado a los 90 días, hemos descubierto una ciclicidad trimestral ligada, por ejemplo, a los vencimientos fiscales, sin tener que adivinarla.
4. Filtrado Digital: Más allá de la Media Móvil
Una vez comprendido el espectro de nuestra señal, debemos limpiarla. La técnica más usada en los negocios es la Media Móvil Simple (SMA). En ingeniería, la SMA se considera un filtro paso bajo muy rudimentario con pésimas características de fase (introduce un retardo, o lag, significativo).
El Problema del Lag
Si usáis una media móvil de 30 días para prever el flujo de caja, vuestro indicador os dirá que la tendencia ha cambiado con 15 días de retraso. En un mercado volátil como el Fintech, este retraso es inaceptable.
La Solución: El Filtro de Kalman
El Filtro de Kalman es el algoritmo definitivo para la estimación de estado en sistemas dinámicos (usado desde el GPS hasta los sistemas de guía de misiles). A diferencia de las medias móviles, el filtro de Kalman no se limita a “suavizar” el pasado, sino que:
- Posee un modelo interno de la física del sistema (ej. la tendencia de crecimiento prevista).
- Compara la previsión del modelo con la nueva medida real (el dato de hoy).
- Calcula la Ganancia de Kalman: decide cuánto confiar en el modelo y cuánto en la nueva medida basándose en la incertidumbre (covarianza) de ambos.
El resultado es una estimación de la tendencia extremadamente reactiva que separa el ruido de la señal real casi en tiempo real, reduciendo drásticamente el lag.
5. Caso de Estudio: Implementación en Python
Veamos cómo aplicar estos conceptos a un dataset ficticio de solicitudes de préstamos diarios.
Paso 1: Análisis Espectral con FFT
import numpy as np
import pandas as pd
from scipy.fft import fft, fftfreq
import matplotlib.pyplot as plt
# Carga de datos (Serie temporal)
data = pd.read_csv('solicitudes_hipotecas.csv')
segnale = data['solicitudes'].values
# Cálculo de la FFT
N = len(segnale)
T = 1.0 / 365.0 # Muestreo diario
yf = fft(segnale)
xf = fftfreq(N, T)[:N//2]
# Gráfico del espectro
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.title('Espectro de Frecuencias (Ciclicidad)')
plt.grid()
plt.show()Interpretación: Los picos en el gráfico indican los ciclos naturales del negocio. Si eliminamos estas frecuencias (filtro notch), obtenemos la tendencia desestacionalizada de manera matemáticamente rigurosa.
Paso 2: Suavizado con Filtro de Kalman
Para limpiar la señal manteniendo la reactividad, usamos una implementación básica de un filtro de Kalman unidimensional.
from pykalman import KalmanFilter
# Configuración del Filtro
# transition_covariance: cuán rápido cambia la tendencia real
# observation_covariance: cuánto ruido hay en los datos diarios
kf = KalmanFilter(transition_matrices=[1],
observation_matrices=[1],
initial_state_mean=segnale[0],
initial_state_covariance=1,
observation_covariance=10,
transition_covariance=0.1)
# Cálculo de la señal filtrada
state_means, _ = kf.filter(segnale)
# Comparación
data['Kalman_Signal'] = state_means
data[['solicitudes', 'Kalman_Signal']].plot()
plt.title('Datos Brutos vs Filtro de Kalman')
plt.show()6. Interpretación de los Resultados para el Negocio
La aplicación de estas técnicas de análisis de series temporales transforma el proceso de toma de decisiones:
- Limpieza del Dato: La línea generada por el filtro de Kalman (
state_means) representa la “verdad” del negocio, depurada de la varianza diaria aleatoria. - Alerta Temprana (Early Warning): Si el dato real se desvía del filtro de Kalman más allá de un cierto umbral (ej. 3 desviaciones estándar de la covarianza residual), no es ruido: es una anomalía o un cambio estructural de mercado que requiere intervención inmediata.
- Previsión (Forecasting): Proyectando el estado del filtro de Kalman en el futuro, obtenemos previsiones de flujo de caja mucho más fiables respecto a la regresión lineal, porque el filtro se adapta dinámicamente a la velocidad de cambio del sistema.
Conclusiones

Tratar los datos de negocio como señales eléctricas no es solo un ejercicio académico, sino una ventaja competitiva. Mientras los competidores reaccionan al ruido (ej. un día de escasas ventas debido al azar), la empresa que utiliza el Signal Processing mantiene el rumbo, reaccionando solo cuando la señal indica un cambio estructural real. El uso de la Transformada de Fourier y del Filtro de Kalman eleva el análisis de las series temporales de simple observación a herramienta predictiva de alta precisión.
Preguntas frecuentes

El Procesamiento de Señales aplicado a los KPI es un enfoque ingenieril que trata los datos de negocio, como las ventas o el flujo de caja, no como simples números estadísticos sino como señales eléctricas. Esta metodología utiliza transformadas matemáticas y filtros digitales para separar la tendencia real, definida como señal, de las fluctuaciones aleatorias del mercado, identificadas como ruido. El objetivo es obtener una visión más clara y científica de la evolución empresarial, depurada de las distorsiones momentáneas.
En el análisis de las series temporales, la Señal representa la información determinista y valiosa, como una tendencia de crecimiento estructural o una estacionalidad recurrente de baja frecuencia. El Ruido, por el contrario, está constituido por variaciones estocásticas y aleatorias, a menudo de alta frecuencia, debidas a factores externos impredecibles como el clima o eventos aislados. Distinguir correctamente la relación Señal Ruido permite evitar decisiones basadas en falsas alarmas.
El Filtro de Kalman es preferible a la Media Móvil Simple porque resuelve el problema del retardo, conocido como lag, típico de los indicadores clásicos. Mientras que la media móvil reacciona lentamente a los cambios suavizando solo los datos pasados, el filtro de Kalman combina un modelo predictivo interno con las mediciones en tiempo real. Esto permite estimar la tendencia actual con extrema reactividad y precisión, adaptándose dinámicamente a la volatilidad del sistema.
La Fast Fourier Transform, o FFT, es fundamental para analizar los datos en el dominio de la frecuencia en lugar de en el del tiempo. Esta herramienta descompone la serie temporal en sus componentes sinusoidales, permitiendo identificar ciclicidades ocultas y estacionalidades complejas, como ciclos semanales o trimestrales, que no serían visibles observando simplemente el gráfico de la evolución temporal de los datos.
Para implementar técnicas de Signal Processing sobre los datos empresariales, el stack tecnológico estándar basado en Python incluye diversas librerías especializadas. NumPy y Pandas son esenciales para la manipulación de las series temporales, mientras que SciPy, en particular el módulo signal, es necesario para calcular transformadas y filtros. Para la implementación específica de los filtros predictivos, se utilizan librerías optimizadas como PyKalman o FilterPy.



¿Te ha resultado útil este artículo? ¿Hay otro tema que te gustaría que tratara?
¡Escríbelo en los comentarios aquí abajo! Me inspiro directamente en vuestras sugerencias.