Kurz gesagt (TL;DR)
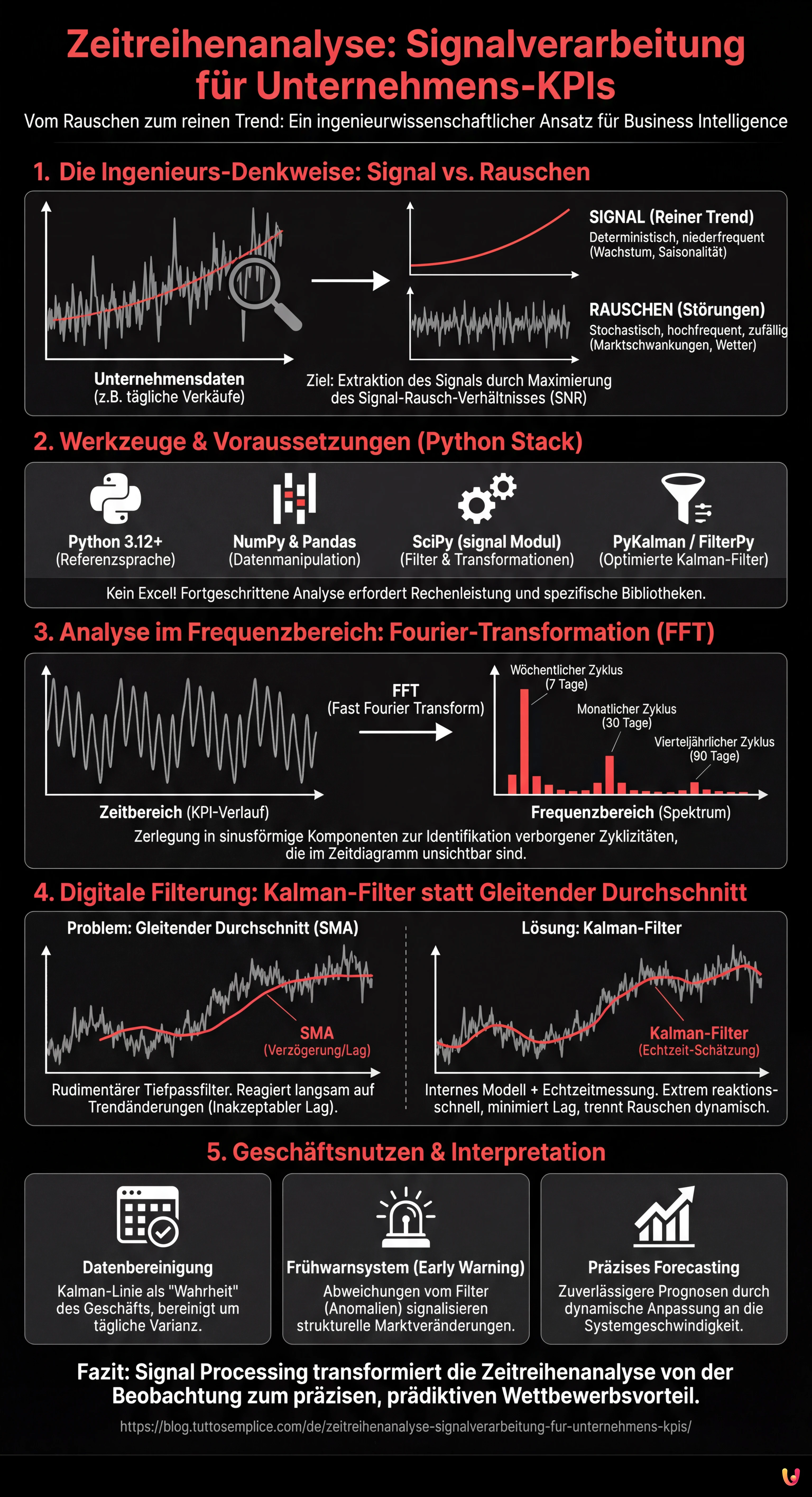
Der Ingenieursansatz verwandelt KPIs in zu verarbeitende Signale und ermöglicht eine klare Trennung strategischer Informationen vom Hintergrundrauschen der Daten.
Die Analyse im Frequenzbereich mit der Fourier-Transformation enthüllt unsichtbare Zyklizitäten und übertrifft Intuitionen, die auf einfacher zeitlicher Beobachtung basieren.
Die Implementierung des Kalman-Filters bietet eine Trendschätzung in Echtzeit und eliminiert die Entscheidungsverzögerung, die durch klassische gleitende Durchschnitte verursacht wird.
Der Teufel steckt im Detail. 👇 Lesen Sie weiter, um die kritischen Schritte und praktischen Tipps zu entdecken, um keine Fehler zu machen.
In der modernen Business Intelligence stellt die Zeitreihenanalyse oft die Grenze zwischen einer auf Intuition basierenden und einer auf Datenwissenschaft fundierten Entscheidung dar. Die meisten Analysten beschränken sich jedoch auf die Beobachtung gleitender Durchschnitte und prozentualer Veränderungen und ignorieren dabei ein methodisches Erbe, das die Elektroniktechnik in den letzten Jahrzehnten perfektioniert hat: das Signal Processing (digitale Signalverarbeitung).
In diesem technischen Leitfaden werden wir den klassischen statistischen Ansatz verlassen und eine ingenieurwissenschaftliche Sichtweise einnehmen. Wir werden Unternehmens-KPIs (wie das Volumen von Hypothekenanfragen in einem Fintech-Unternehmen oder den täglichen Cashflow) nicht als bloße Zahlen in einer Tabellenkalkulation betrachten, sondern als rauschbehaftete elektrische Signale. Durch die Anwendung mathematischer Transformationen und digitaler Filter lernen wir, den “reinen Trend” (das Signal) aus den zufälligen Marktschwankungen (dem Rauschen) zu extrahieren.

1. Die Ingenieurs-Denkweise: Signal vs. Rauschen
In der Elektronik ist ein von einem Sensor empfangenes Signal immer durch externe Störungen verunreinigt. Dasselbe geschieht bei Unternehmensdaten. Wenn wir die Grafik der täglichen Verkäufe betrachten, sehen wir Spitzen und Täler. Die grundlegende Frage lautet: Ist dieser Rückgang am Dienstag ein besorgniserregender Trend (Signal) oder nur eine zufällige Schwankung aufgrund des Wetters oder eines Feiertags (Rauschen)?
Um dies zu beantworten, müssen wir das Signal-Rausch-Verhältnis (SNR – Signal-to-Noise Ratio) definieren. Ein auf der Systemphysik basierender Ansatz lehrt uns:
- Das Signal ist die deterministische Information, oft niederfrequent (Wachstumstrend) oder mit spezifischer Frequenz (Saisonalität).
- Das Rauschen ist stochastisch, oft hochfrequent und zufällig verteilt (weißes Gaußsches Rauschen).
2. Werkzeuge und Voraussetzungen
Um diesem Leitfaden zu folgen, werden wir kein Excel verwenden. Die fortgeschrittene Signalanalyse erfordert Rechenleistung und spezifische Bibliotheken. Im Jahr 2026 umfasst der Standard-Stack für diese Art von Operationen:
- Python 3.12+: Die Referenzsprache.
- NumPy & Pandas: Für die Manipulation von Zeitreihen.
- SciPy (Modul signal): Für die Implementierung digitaler Filter und Transformationen.
- PyKalman oder FilterPy: Optimierte Bibliotheken für die Implementierung von Kalman-Filtern.
3. Analyse im Frequenzbereich: Die Fourier-Transformation (FFT)

Einer der häufigsten Fehler bei der finanziellen Zeitreihenanalyse ist der Versuch, die Saisonalität durch Betrachten des Diagramms im Zeitbereich zu erraten. Ein Elektronikingenieur hingegen verlagert das Problem in den Frequenzbereich.
Mithilfe der Fast Fourier Transform (FFT) können wir unseren KPI (z. B. tägliche Hypothekenanfragen) in seine konstituierenden sinusförmigen Komponenten zerlegen. Dies ermöglicht es uns, verborgene Zyklizitäten zu identifizieren, die das menschliche Auge nicht sieht.
Praktische Anwendung: Erkennung der Zyklizität von Hypotheken
Stellen wir uns vor, wir haben einen Datensatz von 365 Tagen mit Anfragen. Wenn wir die FFT anwenden, könnten wir eine Magnitudenspitze bei der Frequenz sehen, die 7 Tagen entspricht (wöchentlicher Zyklus), und eine bei 30 Tagen (monatlicher Zyklus). Wenn wir eine unerwartete Spitze bei 90 Tagen bemerken, haben wir eine vierteljährliche Zyklizität entdeckt, die beispielsweise mit Steuerfristen zusammenhängt, ohne dass wir sie erraten mussten.
4. Digitale Filterung: Jenseits des gleitenden Durchschnitts
Sobald wir das Spektrum unseres Signals verstanden haben, müssen wir es bereinigen. Die im Geschäftsleben am häufigsten verwendete Technik ist der einfache gleitende Durchschnitt (SMA). In der Technik gilt der SMA als sehr rudimentärer Tiefpassfilter mit schlechten Phaseneigenschaften (er führt eine signifikante Verzögerung oder Lag ein).
Das Problem des Lags
Wenn Sie einen gleitenden 30-Tage-Durchschnitt verwenden, um den Cashflow vorherzusagen, wird Ihnen Ihr Indikator mit 15 Tagen Verspätung mitteilen, dass sich der Trend geändert hat. In einem volatilen Markt wie dem Fintech-Bereich ist diese Verzögerung inakzeptabel.
Die Lösung: Der Kalman-Filter
Der Kalman-Filter ist der definitive Algorithmus zur Zustandsschätzung in dynamischen Systemen (verwendet von GPS bis hin zu Raketenleitsystemen). Im Gegensatz zu gleitenden Durchschnitten beschränkt sich der Kalman-Filter nicht darauf, die Vergangenheit zu “glätten”, sondern:
- Besitzt ein internes Modell der Systemphysik (z. B. der erwartete Wachstumstrend).
- Vergleicht die Vorhersage des Modells mit der neuen realen Messung (dem heutigen Datum).
- Berechnet den Kalman-Gain: Er entscheidet basierend auf der Unsicherheit (Kovarianz) beider, wie sehr er dem Modell und wie sehr der neuen Messung vertraut.
Das Ergebnis ist eine extrem reaktionsschnelle Trendschätzung, die das Rauschen fast in Echtzeit vom realen Signal trennt und den Lag drastisch reduziert.
5. Fallstudie: Implementierung in Python
Sehen wir uns an, wie diese Konzepte auf einen fiktiven Datensatz täglicher Kreditanfragen angewendet werden.
Schritt 1: Spektralanalyse mit FFT
import numpy as np
import pandas as pd
from scipy.fft import fft, fftfreq
import matplotlib.pyplot as plt
# Daten laden (Zeitreihe)
data = pd.read_csv('hypotheken_anfragen.csv')
segnale = data['anfragen'].values
# FFT-Berechnung
N = len(segnale)
T = 1.0 / 365.0 # Tägliche Abtastung
yf = fft(segnale)
xf = fftfreq(N, T)[:N//2]
# Plot des Spektrums
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.title('Frequenzspektrum (Zyklizität)')
plt.grid()
plt.show()Interpretation: Die Spitzen im Diagramm zeigen die natürlichen Geschäftszyklen an. Wenn wir diese Frequenzen eliminieren (Notch-Filter), erhalten wir den saisonbereinigten Trend auf mathematisch rigorose Weise.
Schritt 2: Glättung mit Kalman-Filter
Um das Signal zu bereinigen und gleichzeitig die Reaktionsfähigkeit zu erhalten, verwenden wir eine Basisimplementierung eines eindimensionalen Kalman-Filters.
from pykalman import KalmanFilter
# Konfiguration des Filters
# transition_covariance: wie schnell sich der reale Trend ändert
# observation_covariance: wie viel Rauschen in den täglichen Daten vorhanden ist
kf = KalmanFilter(transition_matrices=[1],
observation_matrices=[1],
initial_state_mean=segnale[0],
initial_state_covariance=1,
observation_covariance=10,
transition_covariance=0.1)
# Berechnung des gefilterten Signals
state_means, _ = kf.filter(segnale)
# Vergleich
data['Kalman_Signal'] = state_means
data[['anfragen', 'Kalman_Signal']].plot()
plt.title('Rohdaten vs. Kalman-Filter')
plt.show()6. Interpretation der Ergebnisse für das Geschäft
Die Anwendung dieser Techniken der Zeitreihenanalyse transformiert den Entscheidungsprozess:
- Datenbereinigung: Die vom Kalman-Filter generierte Linie (
state_means) repräsentiert die “Wahrheit” des Geschäfts, bereinigt um die zufällige tägliche Varianz. - Frühwarnsystem (Early Warning): Wenn die realen Daten über einen bestimmten Schwellenwert (z. B. 3 Standardabweichungen der Restkovarianz) vom Kalman-Filter abweichen, ist dies kein Rauschen: Es ist eine Anomalie oder eine strukturelle Marktveränderung, die sofortiges Eingreifen erfordert.
- Forecasting: Wenn wir den Zustand des Kalman-Filters in die Zukunft projizieren, erhalten wir wesentlich zuverlässigere Cashflow-Prognosen als mit linearer Regression, da sich der Filter dynamisch an die Veränderungsgeschwindigkeit des Systems anpasst.
Fazit

Geschäftsdaten als elektrische Signale zu behandeln, ist nicht nur eine akademische Übung, sondern ein Wettbewerbsvorteil. Während Wettbewerber auf das Rauschen reagieren (z. B. ein Tag mit schlechten Verkäufen aufgrund von Zufall), behält das Unternehmen, das Signal Processing einsetzt, den Kurs bei und reagiert nur, wenn das Signal eine echte strukturelle Veränderung anzeigt. Die Verwendung der Fourier-Transformation und des Kalman-Filters hebt die Zeitreihenanalyse von der einfachen Beobachtung zu einem prädiktiven Instrument von hoher Präzision.
Häufig gestellte Fragen

Signal Processing angewendet auf KPIs ist ein ingenieurwissenschaftlicher Ansatz, der Geschäftsdaten wie Verkäufe oder Cashflow nicht als einfache statistische Zahlen, sondern als elektrische Signale behandelt. Diese Methodik verwendet mathematische Transformationen und digitale Filter, um den realen Trend, definiert als «Signal», von den zufälligen Marktschwankungen, identifiziert als «Rauschen», zu trennen. Das Ziel ist es, eine klarere und wissenschaftlichere Sicht auf die Unternehmensentwicklung zu erhalten, bereinigt um momentane Verzerrungen.
In der Zeitreihenanalyse repräsentiert das Signal die deterministische und wertvolle Information, wie einen strukturellen Wachstumstrend oder eine wiederkehrende Saisonalität mit niedriger Frequenz. Das Rauschen hingegen besteht aus stochastischen und zufälligen Variationen, oft mit hoher Frequenz, die auf unvorhersehbare externe Faktoren wie das Wetter oder isolierte Ereignisse zurückzuführen sind. Das korrekte Unterscheiden des Verhältnisses von Signal zu Rauschen ermöglicht es, Entscheidungen aufgrund falscher Alarme zu vermeiden.
Der Kalman-Filter ist dem einfachen gleitenden Durchschnitt vorzuziehen, da er das Problem der Verzögerung, bekannt als Lag, löst, das typisch für klassische Indikatoren ist. Während der gleitende Durchschnitt langsam auf Änderungen reagiert, indem er nur vergangene Daten glättet, kombiniert der Kalman-Filter ein internes Vorhersagemodell mit Echtzeitmessungen. Dies ermöglicht es, den aktuellen Trend mit extremer Reaktionsfähigkeit und Präzision zu schätzen und sich dynamisch an die Volatilität des Systems anzupassen.
Die Fast Fourier Transform oder FFT ist grundlegend, um Daten im Frequenzbereich anstatt im Zeitbereich zu analysieren. Dieses Werkzeug zerlegt die Zeitreihe in ihre sinusförmigen Komponenten und ermöglicht es, verborgene Zyklizitäten und komplexe Saisonalitäten, wie wöchentliche oder vierteljährliche Zyklen, zu identifizieren, die durch einfaches Betrachten des zeitlichen Verlaufsdiagramms der Daten nicht sichtbar wären.
Um Signal-Processing-Techniken auf Unternehmensdaten zu implementieren, umfasst der auf Python basierende Standard-Technologie-Stack verschiedene spezialisierte Bibliotheken. NumPy und Pandas sind essenziell für die Manipulation von Zeitreihen, während SciPy, insbesondere das Modul signal, für die Berechnung von Transformationen und Filtern notwendig ist. Für die spezifische Implementierung von prädiktiven Filtern werden optimierte Bibliotheken wie PyKalman oder FilterPy verwendet.



Fanden Sie diesen Artikel hilfreich? Gibt es ein anderes Thema, das Sie von mir behandelt sehen möchten?
Schreiben Sie es in die Kommentare unten! Ich lasse mich direkt von Ihren Vorschlägen inspirieren.