Filtro di Kalman: Guida Tecnica per Finanza e Lead Scoring

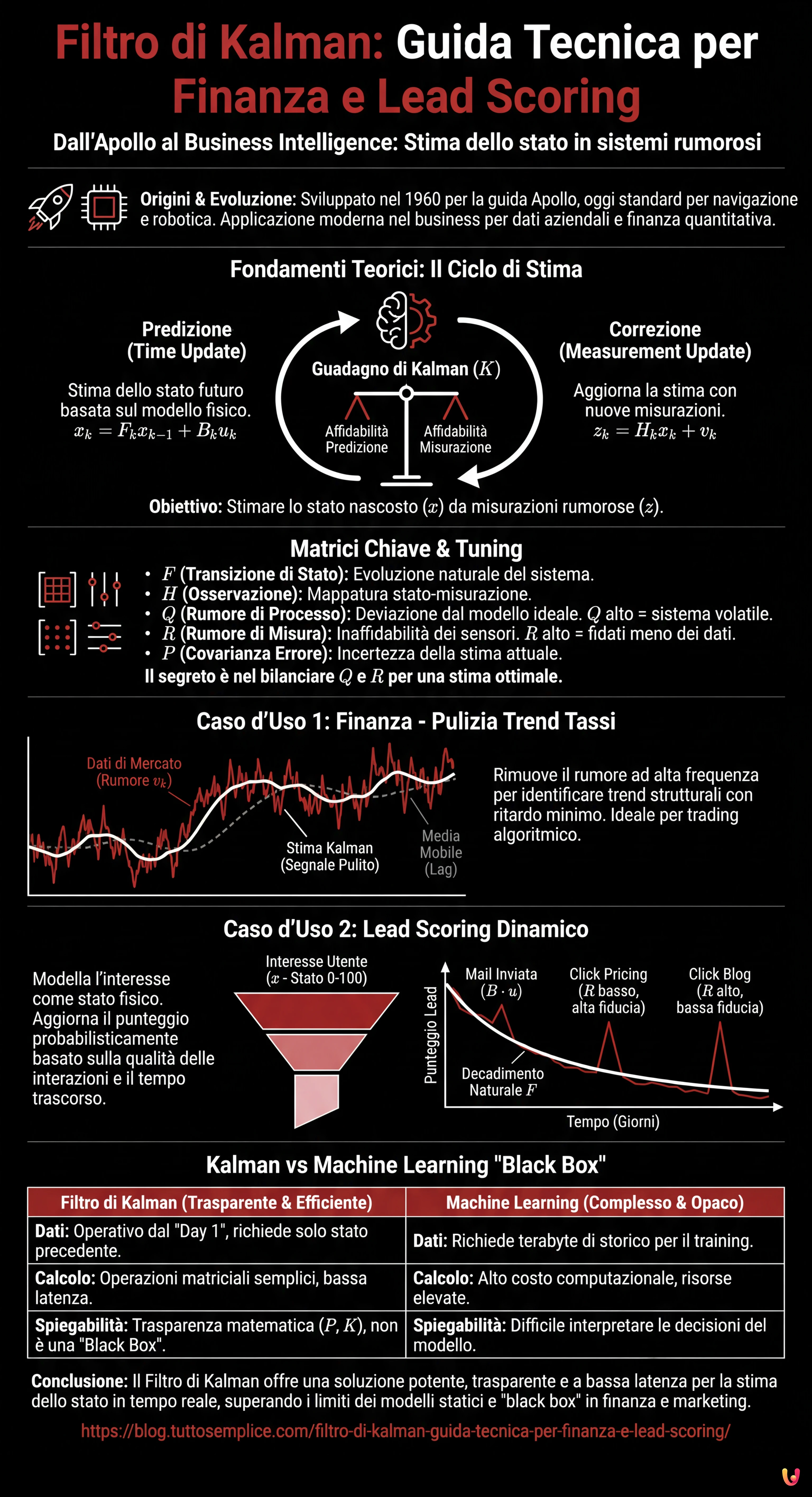
Il filtro di Kalman è una delle pietre miliari della teoria del controllo e dell’ingegneria dei sistemi. Originariamente sviluppato da Rudolf E. Kalman nel 1960 e reso celebre dal suo utilizzo nel computer di guida delle missioni Apollo, questo algoritmo ricorsivo è lo standard de facto per la stima dello stato in sistemi rumorosi, dalla navigazione GPS alla robotica. Tuttavia, nel 2026, la sua applicazione ha trasceso l’hardware per approdare con prepotenza nel mondo del business intelligence e della finanza quantitativa.

In questo articolo tecnico, abbandoneremo le metafore superficiali per concentrarci sull’ingegneria pura applicata ai dati aziendali. Vedremo come configurare un filtro di Kalman per due scopi critici: la pulizia del segnale nei trend dei tassi di interesse (rimuovendo il rumore di mercato ad alta frequenza) e la stima dinamica della qualità dei lead (Lead Scoring) in tempo reale. A differenza dei modelli di Machine Learning “black box”, il filtro di Kalman offre trasparenza matematica e una latenza quasi nulla, rendendolo ideale per sistemi decisionali automatizzati.

Fondamenti Teorici: Perché il Filtro di Kalman?

Il problema fondamentale che il filtro risolve è la stima dello stato nascosto di un sistema ($x$) basandosi su misurazioni osservabili ($z$) che sono affette da rumore. In un contesto business:

• Lo Stato ($x$): È la “verità” che vogliamo conoscere. Esempio: il vero interesse di un cliente (Lead Score) o il trend strutturale di un tasso di cambio.
• La Misurazione ($z$): È ciò che vediamo. Esempio: un click su una mail (che potrebbe essere accidentale) o il prezzo di chiusura giornaliero (affetto da volatilità speculativa).

Il filtro opera in un ciclo a due fasi: Predizione (Time Update) e Correzione (Measurement Update). La sua potenza risiede nella capacità di pesare l’affidabilità della nostra predizione matematica contro l’affidabilità della nuova misurazione, attraverso una variabile calcolata dinamicamente chiamata Guadagno di Kalman ($K$).

Configurazione Matematica delle Matrici

Per implementare il filtro, dobbiamo definire le equazioni di stato. Assumiamo un sistema lineare discreto:

$$x_k = F_k x_{k-1} + B_k u_k + w_k$$

$$z_k = H_k x_k + v_k$$

Dove:

• $F$ (Matrice di Transizione di Stato): Come lo stato evolve da solo nel tempo.
• $H$ (Matrice di Osservazione): Come lo stato viene mappato nella misurazione.
• $Q$ (Covarianza del Rumore di Processo): Quanto il sistema reale devia dal modello ideale ($w_k$).
• $R$ (Covarianza del Rumore di Misura): Quanto sono inaffidabili i nostri sensori/dati ($v_k$).
• $P$ (Covarianza dell’Errore di Stima): La nostra incertezza attuale sulla stima dello stato.

Il Segreto è in Q ed R

La “magia” ingegneristica sta nel tuning di $Q$ e $R$. Se impostiamo un $R$ alto, diciamo al filtro: “Non fidarti troppo delle misurazioni, sono rumorose; fidati di più della predizione storica”. Se impostiamo un $Q$ alto, diciamo: “Il sistema è molto volatile, cambia direzione rapidamente”.

Caso d’Uso 1: Previsione e Pulizia dei Tassi di Interesse

I mercati finanziari sono rumorosi. Una media mobile (Moving Average) introduce un ritardo (lag) inaccettabile per il trading ad alta frequenza. Il filtro di Kalman, invece, stima lo stato corrente minimizzando l’errore quadratico medio, offrendo un segnale “pulito” con un ritardo minimo.

Configurazione del Modello

Immaginiamo di tracciare l’EUR/USD. Consideriamo lo stato $x$ come una coppia [Prezzo, Velocità].

• Matrice $F$: Modella la fisica del prezzo. Se assumiamo velocità costante:
  $$F = begin{bmatrix} 1 & Delta t 0 & 1 end{bmatrix}$$
• Matrice $H$: Osserviamo solo il prezzo, non la velocità direttamente.
  $$H = begin{bmatrix} 1 & 0 end{bmatrix}$$
• Matrice $R$: Calcolata sulla varianza storica del rumore intraday.

Applicando questo filtro, otteniamo una curva che ignora gli spike speculativi (rumore $v_k$) ma reagisce prontamente ai cambi di trend strutturali (dinamica di sistema), permettendo di identificare inversioni di mercato prima di una media mobile esponenziale (EMA).

Caso d’Uso 2: Lead Scoring Dinamico nel Funnel

Nel marketing B2B, il Lead Scoring tradizionale è statico (es. “Ha scaricato l’ebook = +5 punti”). Questo approccio ignora il decadimento dell’interesse nel tempo e l’incertezza delle azioni utente. Possiamo modellare l’interesse di un utente come uno stato fisico che si muove nello spazio.

Modellazione dell’Intento Utente

Definiamo lo stato $x$ come un valore scalare continuo da 0 a 100 (Livello di Interesse).

1. Dinamica del Processo ($F$): L’interesse decade naturalmente nel tempo se non alimentato. Possiamo impostare $F = 0.95$ (decadimento esponenziale giornaliero).
2. Input di Controllo ($B cdot u$): Le azioni di marketing (es. invio di una mail) sono forze esterne che spingono lo stato verso l’alto.
3. Misurazioni ($z$): Le interazioni dell’utente (click, visite al sito).
4. Rumore di Misura ($R$): Qui sta la genialità. Non tutti i click sono uguali.
   • Click su “Pricing Page”: $R$ basso (alta confidenza, segnale forte).
   • Click su “Blog Post generico”: $R$ alto (bassa confidenza, molto rumore).

Il filtro aggiornerà il punteggio del lead in modo probabilistico. Se un utente visita la pagina prezzi (misurazione forte), il filtro alzerà drasticamente la stima e ridurrà la matrice di covarianza $P$ (maggiore certezza). Se l’utente sparisce per due settimane, la dinamica $F$ farà decadere il punteggio, e $P$ aumenterà (siamo meno sicuri del suo stato).

Implementazione Pratica in Python

Ecco un esempio semplificato utilizzando la libreria numpy per implementare un filtro monodimensionale per il Lead Scoring.

import numpy as np

class KalmanFilter:
    def __init__(self, F, B, H, Q, R, P, x):
        self.F = F  # Transizione di stato
        self.B = B  # Matrice di controllo
        self.H = H  # Matrice di osservazione
        self.Q = Q  # Rumore di processo
        self.R = R  # Rumore di misura
        self.P = P  # Covarianza errore
        self.x = x  # Stato iniziale

    def predict(self, u=0):
        # Predizione dello stato
        self.x = self.F * self.x + self.B * u
        # Predizione della covarianza
        self.P = self.F * self.P * self.F + self.Q
        return self.x

    def update(self, z):
        # Calcolo del residuo di misura
        y = z - self.H * self.x
        # Calcolo del guadagno di Kalman (K)
        S = self.H * self.P * self.H + self.R
        K = self.P * self.H / S
        
        # Aggiornamento stato e covarianza
        self.x = self.x + K * y
        self.P = (1 - K * self.H) * self.P
        return self.x

# Configurazione per Lead Scoring
# Stato iniziale: 50/100, Incertezza P alta
kf = KalmanFilter(F=0.98, B=5, H=1, Q=0.1, R=10, P=100, x=50)

# Giorno 1: Nessuna azione (Decadimento)
print(f"Giorno 1 (No azioni): {kf.predict(u=0):.2f}")

# Giorno 2: Utente visita Pricing (Misurazione z=90, R basso dinamico)
kf.R = 2 # Alta fiducia
kf.predict(u=0)
print(f"Giorno 2 (Visita Pricing): {kf.update(z=90):.2f}")

Kalman vs Machine Learning: Perché scegliere il primo?

Nell’era dell’Intelligenza Artificiale generativa e delle reti neurali profonde, perché tornare a un algoritmo del 1960? La risposta risiede nell’efficienza e nella spiegabilità.

• Dati necessari: Le reti neurali richiedono terabyte di dati storici per il training. Il filtro di Kalman richiede solo lo stato precedente e la misurazione attuale. È operativo dal “Day 1”.
• Costo Computazionale: Il filtro di Kalman è costituito da semplici operazioni matriciali. Può girare su microcontrollori o server sovraccarichi con latenza trascurabile.
• Trasparenza: Se il modello sbaglia, possiamo ispezionare la matrice $P$ o il guadagno $K$ per capire esattamente perché. Non è una “Black Box”.

Conclusioni

Applicare il filtro di Kalman al di fuori dell’ingegneria elettronica richiede un cambio di paradigma: bisogna smettere di vedere i dati business come semplici numeri e iniziare a vederli come segnali emessi da un sistema dinamico. Che si tratti di prevedere la traiettoria di un missile o la propensione all’acquisto di un cliente, la matematica della stima dello stato rimane la stessa. Per le aziende che cercano vantaggi competitivi in tempo reale, la padronanza di questi strumenti di controllo offre un vantaggio strategico netto rispetto ai concorrenti che si affidano ancora a medie statiche o a modelli ML opachi e lenti.

Domande frequenti

Fonti e Approfondimenti

1. Wikipedia: Definizione matematica e funzionamento del Filtro di Kalman
2. NASA History Division: L’implementazione del Filtro di Kalman nel computer di guida Apollo
3. Federal Reserve: Applicazione di modelli di filtraggio per la stima dei trend dei tassi di interesse

Francesco Zinghinì

Ingegnere Elettronico con la missione di semplificare il digitale. Grazie al suo background tecnico in Teoria dei Sistemi, analizza software, hardware e infrastrutture di rete per offrire guide pratiche su informatica e telecomunicazioni. Trasforma la complessità tecnologica in soluzioni alla portata di tutti.

LinkedInFacebookBio Completa →