Kalman-Filter: Technischer Leitfaden für Finanzen und Lead Scoring

Der Kalman-Filter ist einer der Grundpfeiler der Regelungstheorie und der Systemtechnik. Ursprünglich 1960 von Rudolf E. Kalman entwickelt und durch seinen Einsatz im Leitrechner der Apollo-Missionen berühmt geworden, ist dieser rekursive Algorithmus der De-facto-Standard für die Zustandsschätzung in verrauschten Systemen, von der GPS-Navigation bis zur Robotik. Im Jahr 2026 hat seine Anwendung jedoch die Hardware transzendiert und mit Wucht Einzug in die Welt der Business Intelligence und der quantitativen Finanzen gehalten.

In diesem technischen Artikel lassen wir oberflächliche Metaphern hinter uns und konzentrieren uns auf reine Ingenieurskunst, angewandt auf Unternehmensdaten. Wir werden sehen, wie man einen Kalman-Filter für zwei kritische Zwecke konfiguriert: die Signalbereinigung bei Zinstrends (durch Entfernung von hochfrequentem Marktrauschen) und die dynamische Schätzung der Lead-Qualität (Lead Scoring) in Echtzeit. Im Gegensatz zu „Black Box“-Modellen des maschinellen Lernens bietet der Kalman-Filter mathematische Transparenz und eine Latenz von nahezu Null, was ihn ideal für automatisierte Entscheidungssysteme macht.

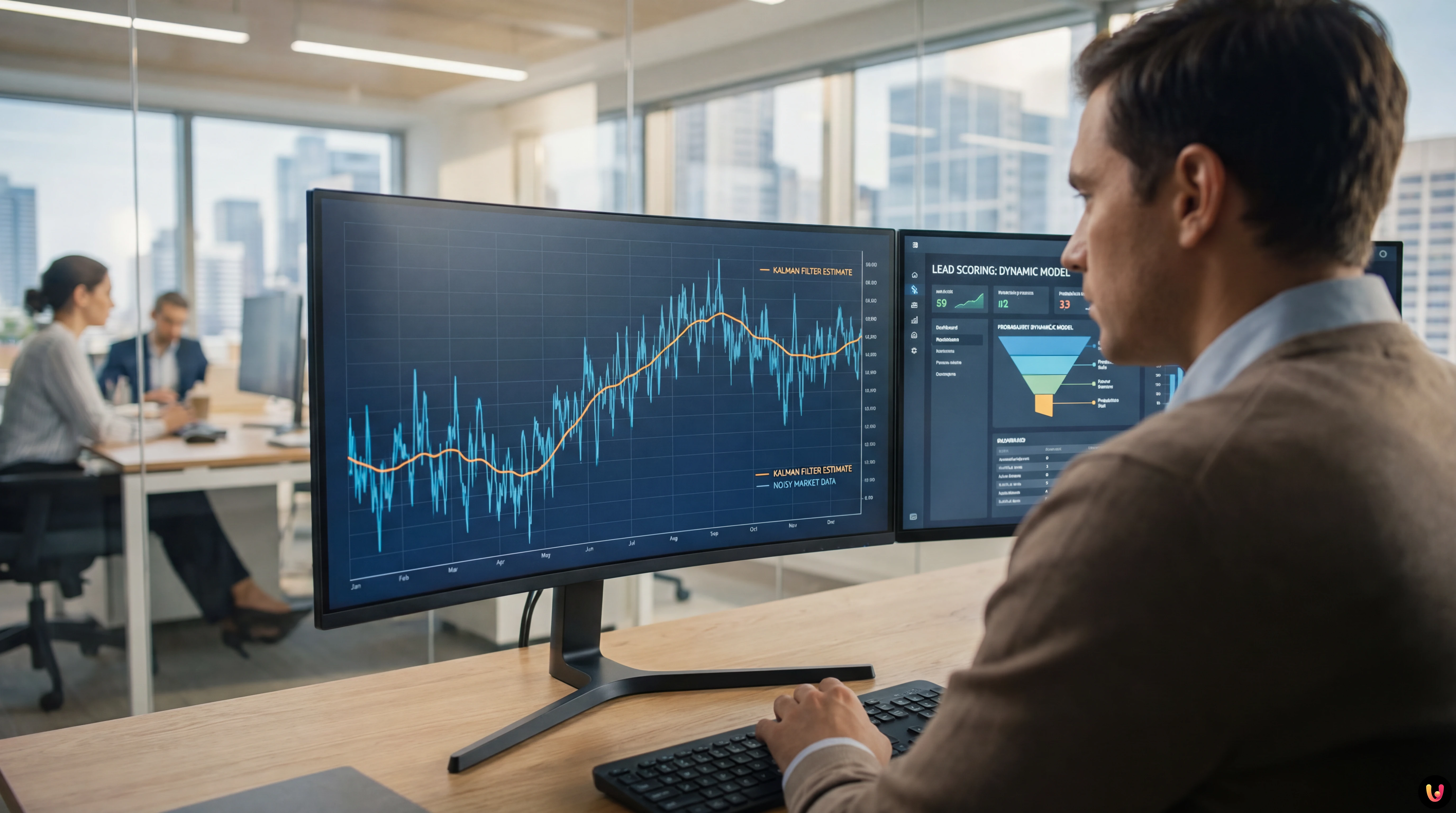
Theoretische Grundlagen: Warum der Kalman-Filter?

Das grundlegende Problem, das der Filter löst, ist die Schätzung des verborgenen Zustands eines Systems ($x$) auf der Grundlage von beobachtbaren Messungen ($z$), die mit Rauschen behaftet sind. In einem geschäftlichen Kontext:

• Der Zustand ($x$): Dies ist die „Wahrheit“, die wir kennen wollen. Beispiel: das wahre Interesse eines Kunden (Lead Score) oder der strukturelle Trend eines Wechselkurses.
• Die Messung ($z$): Das ist das, was wir sehen. Beispiel: ein Klick auf eine E-Mail (der versehentlich sein könnte) oder der tägliche Schlusskurs (beeinflusst durch spekulative Volatilität).

Der Filter arbeitet in einem zweistufigen Zyklus: Vorhersage (Time Update) und Korrektur (Measurement Update). Seine Stärke liegt in der Fähigkeit, die Zuverlässigkeit unserer mathematischen Vorhersage gegen die Zuverlässigkeit der neuen Messung abzuwägen, und zwar durch eine dynamisch berechnete Variable namens Kalman-Gain ($K$).

Mathematische Konfiguration der Matrizen

Um den Filter zu implementieren, müssen wir die Zustandsgleichungen definieren. Wir gehen von einem linearen diskreten System aus:

$$x_k = F_k x_{k-1} + B_k u_k + w_k$$

$$z_k = H_k x_k + v_k$$

Wobei:

• $F$ (Zustandsübergangsmatrix): Wie sich der Zustand im Laufe der Zeit von selbst entwickelt.
• $H$ (Beobachtungsmatrix): Wie der Zustand auf die Messung abgebildet wird.
• $Q$ (Prozessrauschkovarianz): Wie stark das reale System vom idealen Modell abweicht ($w_k$).
• $R$ (Messrauschkovarianz): Wie unzuverlässig unsere Sensoren/Daten sind ($v_k$).
• $P$ (Schätzfehlerkovarianz): Unsere aktuelle Unsicherheit über die Zustandsschätzung.

Das Geheimnis liegt in Q und R

Die „Magie“ der Ingenieurskunst liegt in der Feinabstimmung von $Q$ und $R$. Wenn wir ein hohes $R$ einstellen, sagen wir dem Filter: „Traue den Messungen nicht zu sehr, sie sind verrauscht; vertraue mehr der historischen Vorhersage“. Wenn wir ein hohes $Q$ einstellen, sagen wir: „Das System ist sehr volatil, es ändert die Richtung schnell“.

Anwendungsfall 1: Vorhersage und Bereinigung von Zinssätzen

Finanzmärkte sind verrauscht. Ein gleitender Durchschnitt (Moving Average) führt eine Verzögerung (Lag) ein, die für den Hochfrequenzhandel inakzeptabel ist. Der Kalman-Filter hingegen schätzt den aktuellen Zustand durch Minimierung des mittleren quadratischen Fehlers und bietet ein „sauberes“ Signal mit minimaler Verzögerung.

Konfiguration des Modells

Stellen wir uns vor, wir verfolgen den EUR/USD-Kurs. Wir betrachten den Zustand $x$ als ein Paar [Preis, Geschwindigkeit].

• Matrix $F$: Modelliert die Physik des Preises. Wenn wir eine konstante Geschwindigkeit annehmen:
  $$F = begin{bmatrix} 1 & Delta t 0 & 1 end{bmatrix}$$
• Matrix $H$: Wir beobachten nur den Preis, nicht die Geschwindigkeit direkt.
  $$H = begin{bmatrix} 1 & 0 end{bmatrix}$$
• Matrix $R$: Berechnet auf der historischen Varianz des Intraday-Rauschens.

Durch Anwendung dieses Filters erhalten wir eine Kurve, die spekulative Spitzen (Rauschen $v_k$) ignoriert, aber prompt auf strukturelle Trendänderungen (Systemdynamik) reagiert, was es ermöglicht, Marktumkehrungen früher als ein exponentieller gleitender Durchschnitt (EMA) zu identifizieren.

Anwendungsfall 2: Dynamisches Lead Scoring im Funnel

Im B2B-Marketing ist das traditionelle Lead Scoring statisch (z. B. „E-Book heruntergeladen = +5 Punkte“). Dieser Ansatz ignoriert den Interessenzerfall im Laufe der Zeit und die Unsicherheit von Nutzeraktionen. Wir können das Interesse eines Nutzers als einen physikalischen Zustand modellieren, der sich im Raum bewegt.

Modellierung der Nutzerabsicht

Wir definieren den Zustand $x$ als einen kontinuierlichen skalaren Wert von 0 bis 100 (Interessenniveau).

1. Prozessdynamik ($F$): Das Interesse zerfällt natürlich mit der Zeit, wenn es nicht genährt wird. Wir können $F = 0.95$ setzen (täglicher exponentieller Zerfall).
2. Steuereingang ($B cdot u$): Marketingaktionen (z. B. Senden einer E-Mail) sind externe Kräfte, die den Zustand nach oben treiben.
3. Messungen ($z$): Die Interaktionen des Nutzers (Klicks, Website-Besuche).
4. Messrauschen ($R$): Hier liegt der Clou. Nicht alle Klicks sind gleich.
   • Klick auf „Preisseite“: $R$ niedrig (hohes Vertrauen, starkes Signal).
   • Klick auf „Allgemeiner Blogpost“: $R$ hoch (geringes Vertrauen, viel Rauschen).

Der Filter aktualisiert den Lead-Score probabilistisch. Wenn ein Nutzer die Preisseite besucht (starke Messung), hebt der Filter die Schätzung drastisch an und reduziert die Kovarianzmatrix $P$ (höhere Gewissheit). Wenn der Nutzer für zwei Wochen verschwindet, lässt die Dynamik $F$ den Score zerfallen, und $P$ steigt (wir sind uns seines Zustands weniger sicher).

Praktische Implementierung in Python

Hier ist ein vereinfachtes Beispiel unter Verwendung der Bibliothek numpy zur Implementierung eines eindimensionalen Filters für das Lead Scoring.

import numpy as np

class KalmanFilter:
    def __init__(self, F, B, H, Q, R, P, x):
        self.F = F  # Zustandsübergang
        self.B = B  # Steuermatrix
        self.H = H  # Beobachtungsmatrix
        self.Q = Q  # Prozessrauschen
        self.R = R  # Messrauschen
        self.P = P  # Fehlerkovarianz
        self.x = x  # Anfangszustand

    def predict(self, u=0):
        # Zustandsvorhersage
        self.x = self.F * self.x + self.B * u
        # Kovarianzvorhersage
        self.P = self.F * self.P * self.F + self.Q
        return self.x

    def update(self, z):
        # Berechnung des Messresiduums
        y = z - self.H * self.x
        # Berechnung des Kalman-Gain (K)
        S = self.H * self.P * self.H + self.R
        K = self.P * self.H / S
        
        # Aktualisierung von Zustand und Kovarianz
        self.x = self.x + K * y
        self.P = (1 - K * self.H) * self.P
        return self.x

# Konfiguration für Lead Scoring
# Anfangszustand: 50/100, Unsicherheit P hoch
kf = KalmanFilter(F=0.98, B=5, H=1, Q=0.1, R=10, P=100, x=50)

# Tag 1: Keine Aktion (Zerfall)
print(f"Tag 1 (Keine Aktionen): {kf.predict(u=0):.2f}")

# Tag 2: Nutzer besucht Preise (Messung z=90, R niedrig dynamisch)
kf.R = 2 # Hohes Vertrauen
kf.predict(u=0)
print(f"Tag 2 (Besuch Preise): {kf.update(z=90):.2f}")

Kalman vs. Machine Learning: Warum Ersteres wählen?

Warum sollte man im Zeitalter der generativen künstlichen Intelligenz und tiefer neuronaler Netze zu einem Algorithmus von 1960 zurückkehren? Die Antwort liegt in der Effizienz und Erklärbarkeit.

• Notwendige Daten: Neuronale Netze benötigen Terabytes an historischen Daten für das Training. Der Kalman-Filter benötigt nur den vorherigen Zustand und die aktuelle Messung. Er ist ab „Tag 1“ einsatzbereit.
• Rechenaufwand: Der Kalman-Filter besteht aus einfachen Matrixoperationen. Er kann auf Mikrocontrollern oder überlasteten Servern mit vernachlässigbarer Latenz laufen.
• Transparenz: Wenn das Modell falsch liegt, können wir die Matrix $P$ oder den Gain $K$ inspizieren, um genau zu verstehen, warum. Es ist keine „Black Box“.

Fazit

Die Anwendung des Kalman-Filters außerhalb der Elektrotechnik erfordert einen Paradigmenwechsel: Man muss aufhören, Geschäftsdaten als einfache Zahlen zu sehen, und beginnen, sie als Signale zu betrachten, die von einem dynamischen System ausgesendet werden. Ob es darum geht, die Flugbahn einer Rakete oder die Kaufneigung eines Kunden vorherzusagen, die Mathematik der Zustandsschätzung bleibt dieselbe. Für Unternehmen, die Wettbewerbsvorteile in Echtzeit suchen, bietet die Beherrschung dieser Steuerungsinstrumente einen klaren strategischen Vorteil gegenüber Wettbewerbern, die sich noch auf statische Durchschnittswerte oder undurchsichtige und langsame ML-Modelle verlassen.

Häufig gestellte Fragen

Quellen und Vertiefung

1. Wikipedia: Definition und mathematische Grundlagen des Kalman-Filters
2. Deutsche Bundesbank: Offizielle Statistiken zu Zinssätzen und Renditen (Datenbasis für Finanzanalysen)
3. NASA History Division: Historischer Hintergrund zur Apollo-Mission und Navigationstechnologie
4. Wikipedia: Biografie des Mathematikers Rudolf E. Kálmán

Francesco Zinghinì

Elektronikingenieur mit der Mission, die digitale Welt zu vereinfachen. Dank seines technischen Hintergrunds in Systemtheorie analysiert er Software, Hardware und Netzwerkinfrastrukturen, um praktische Leitfäden zu IT und Telekommunikation anzubieten. Er verwandelt technische Komplexität in für alle zugängliche Lösungen.

LinkedInFacebookVollständige Biografie →