Filtre de Kalman : Guide Technique pour la Finance et le Lead Scoring

Le filtre de Kalman est l’une des pierres angulaires de la théorie du contrôle et de l’ingénierie des systèmes. Développé à l’origine par Rudolf E. Kalman en 1960 et rendu célèbre par son utilisation dans l’ordinateur de guidage des missions Apollo, cet algorithme récursif est la norme de facto pour l’estimation d’état dans les systèmes bruyants, de la navigation GPS à la robotique. Cependant, en 2026, son application a transcendé le matériel pour s’imposer avec force dans le monde de la Business Intelligence et de la finance quantitative.

Dans cet article technique, nous abandonnerons les métaphores superficielles pour nous concentrer sur l’ingénierie pure appliquée aux données d’entreprise. Nous verrons comment configurer un filtre de Kalman pour deux objectifs critiques : le nettoyage du signal dans les tendances des taux d’intérêt (en supprimant le bruit de marché à haute fréquence) et l’estimation dynamique de la qualité des leads (Lead Scoring) en temps réel. Contrairement aux modèles de Machine Learning de type « boîte noire », le filtre de Kalman offre une transparence mathématique et une latence quasi nulle, ce qui le rend idéal pour les systèmes décisionnels automatisés.

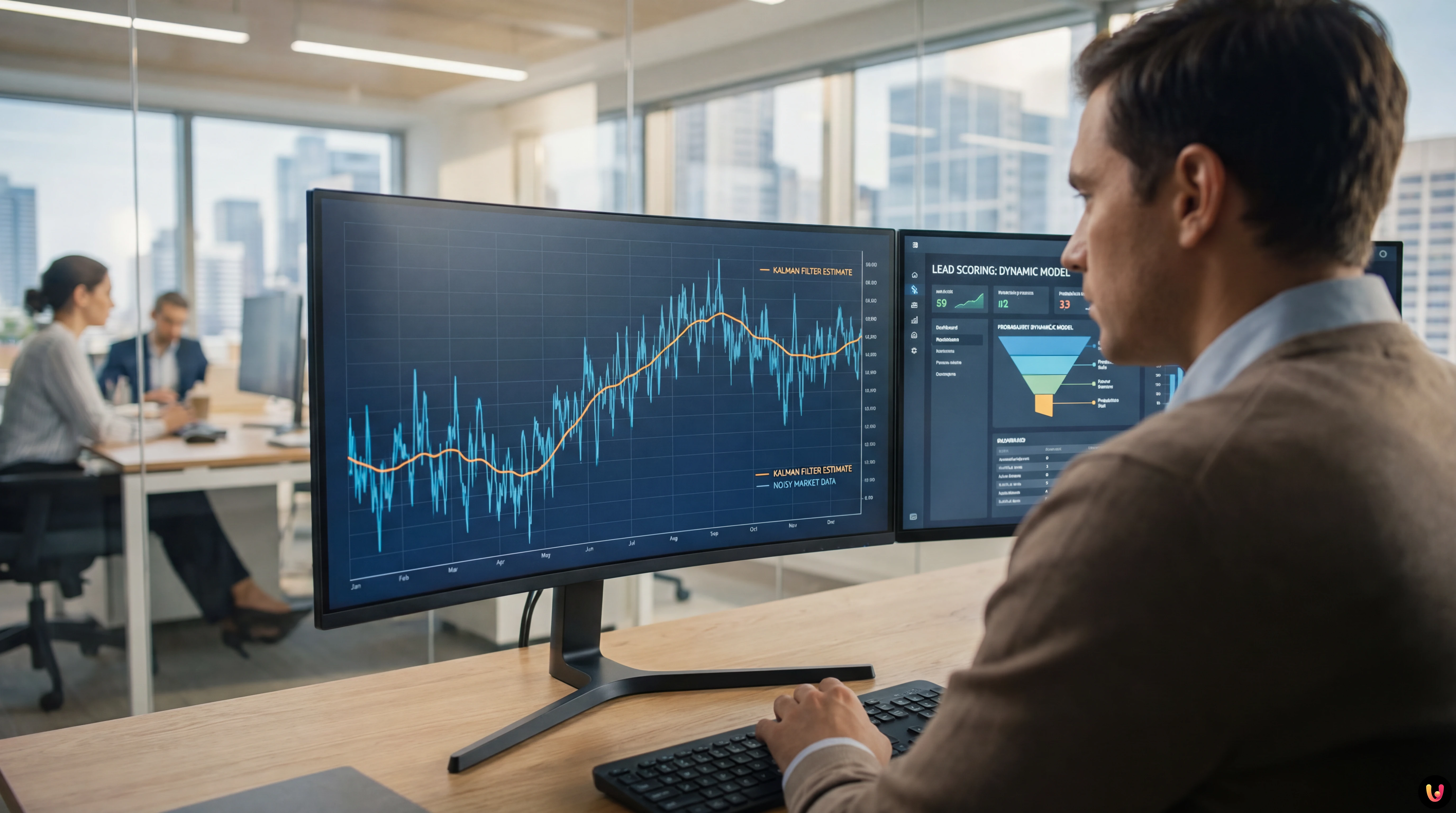
Fondements Théoriques : Pourquoi le Filtre de Kalman ?

Le problème fondamental que le filtre résout est l’estimation de l’état caché d’un système ($x$) en se basant sur des mesures observables ($z$) qui sont affectées par du bruit. Dans un contexte business :

• L’État ($x$) : C’est la « vérité » que nous voulons connaître. Exemple : le véritable intérêt d’un client (Lead Score) ou la tendance structurelle d’un taux de change.
• La Mesure ($z$) : C’est ce que nous voyons. Exemple : un clic sur un e-mail (qui pourrait être accidentel) ou le prix de clôture quotidien (affecté par la volatilité spéculative).

Le filtre opère selon un cycle en deux phases : Prédiction (Time Update) et Correction (Measurement Update). Sa puissance réside dans sa capacité à pondérer la fiabilité de notre prédiction mathématique par rapport à la fiabilité de la nouvelle mesure, grâce à une variable calculée dynamiquement appelée Gain de Kalman ($K$).

Configuration Mathématique des Matrices

Pour implémenter le filtre, nous devons définir les équations d’état. Supposons un système linéaire discret :

$$x_k = F_k x_{k-1} + B_k u_k + w_k$$

$$z_k = H_k x_k + v_k$$

Où :

• $F$ (Matrice de Transition d’État) : Comment l’état évolue de lui-même dans le temps.
• $H$ (Matrice d’Observation) : Comment l’état est mappé dans la mesure.
• $Q$ (Covariance du Bruit de Processus) : À quel point le système réel dévie du modèle idéal ($w_k$).
• $R$ (Covariance du Bruit de Mesure) : À quel point nos capteurs/données sont peu fiables ($v_k$).
• $P$ (Covariance de l’Erreur d’Estimation) : Notre incertitude actuelle sur l’estimation de l’état.

Le Secret réside dans Q et R

La « magie » de l’ingénierie réside dans le réglage de $Q$ et $R$. Si nous définissons un $R$ élevé, nous disons au filtre : « Ne te fie pas trop aux mesures, elles sont bruyantes ; fie-toi davantage à la prédiction historique ». Si nous définissons un $Q$ élevé, nous disons : « Le système est très volatil, il change de direction rapidement ».

Cas d’Usage 1 : Prévision et Nettoyage des Taux d’Intérêt

Les marchés financiers sont bruyants. Une moyenne mobile (Moving Average) introduit un retard (lag) inacceptable pour le trading à haute fréquence. Le filtre de Kalman, en revanche, estime l’état actuel en minimisant l’erreur quadratique moyenne, offrant un signal « propre » avec un retard minimal.

Configuration du Modèle

Imaginons que nous suivons l’EUR/USD. Considérons l’état $x$ comme une paire [Prix, Vitesse].

• Matrice $F$ : Modélise la physique du prix. Si nous supposons une vitesse constante :
  $$F = begin{bmatrix} 1 & Delta t 0 & 1 end{bmatrix}$$
• Matrice $H$ : Nous observons seulement le prix, pas la vitesse directement.
  $$H = begin{bmatrix} 1 & 0 end{bmatrix}$$
• Matrice $R$ : Calculée sur la variance historique du bruit intraday.

En appliquant ce filtre, nous obtenons une courbe qui ignore les pics spéculatifs (bruit $v_k$) mais réagit promptement aux changements de tendance structurels (dynamique du système), permettant d’identifier les retournements de marché avant une moyenne mobile exponentielle (EMA).

Cas d’Usage 2 : Lead Scoring Dynamique dans le Funnel

Dans le marketing B2B, le Lead Scoring traditionnel est statique (ex. « A téléchargé l’ebook = +5 points »). Cette approche ignore la décroissance de l’intérêt dans le temps et l’incertitude des actions de l’utilisateur. Nous pouvons modéliser l’intérêt d’un utilisateur comme un état physique se déplaçant dans l’espace.

Modélisation de l’Intention Utilisateur

Définissons l’état $x$ comme une valeur scalaire continue de 0 à 100 (Niveau d’Intérêt).

1. Dynamique du Processus ($F$) : L’intérêt décroît naturellement avec le temps s’il n’est pas alimenté. Nous pouvons définir $F = 0.95$ (décroissance exponentielle quotidienne).
2. Entrée de Contrôle ($B cdot u$) : Les actions marketing (ex. envoi d’un e-mail) sont des forces externes qui poussent l’état vers le haut.
3. Mesures ($z$) : Les interactions de l’utilisateur (clics, visites sur le site).
4. Bruit de Mesure ($R$) : C’est ici que réside le génie. Tous les clics ne se valent pas.
   • Clic sur « Page Tarifs » : $R$ bas (haute confiance, signal fort).
   • Clic sur « Article de Blog générique » : $R$ élevé (faible confiance, beaucoup de bruit).

Le filtre mettra à jour le score du lead de manière probabiliste. Si un utilisateur visite la page des tarifs (mesure forte), le filtre augmentera considérablement l’estimation et réduira la matrice de covariance $P$ (plus grande certitude). Si l’utilisateur disparaît pendant deux semaines, la dynamique $F$ fera décroître le score, et $P$ augmentera (nous sommes moins sûrs de son état).

Implémentation Pratique en Python

Voici un exemple simplifié utilisant la bibliothèque numpy pour implémenter un filtre monodimensionnel pour le Lead Scoring.

import numpy as np

class KalmanFilter:
    def __init__(self, F, B, H, Q, R, P, x):
        self.F = F  # Transition d'état
        self.B = B  # Matrice de contrôle
        self.H = H  # Matrice d'observation
        self.Q = Q  # Bruit de processus
        self.R = R  # Bruit de mesure
        self.P = P  # Covariance erreur
        self.x = x  # État initial

    def predict(self, u=0):
        # Prédiction de l'état
        self.x = self.F * self.x + self.B * u
        # Prédiction de la covariance
        self.P = self.F * self.P * self.F + self.Q
        return self.x

    def update(self, z):
        # Calcul du résidu de mesure
        y = z - self.H * self.x
        # Calcul du gain de Kalman (K)
        S = self.H * self.P * self.H + self.R
        K = self.P * self.H / S
        
        # Mise à jour état et covariance
        self.x = self.x + K * y
        self.P = (1 - K * self.H) * self.P
        return self.x

# Configuration pour Lead Scoring
# État initial : 50/100, Incertitude P élevée
kf = KalmanFilter(F=0.98, B=5, H=1, Q=0.1, R=10, P=100, x=50)

# Jour 1 : Aucune action (Décroissance)
print(f"Jour 1 (Pas d'actions) : {kf.predict(u=0):.2f}")

# Jour 2 : Utilisateur visite Tarifs (Mesure z=90, R bas dynamique)
kf.R = 2 # Haute confiance
kf.predict(u=0)
print(f"Jour 2 (Visite Tarifs) : {kf.update(z=90):.2f}")

Kalman vs Machine Learning : Pourquoi choisir le premier ?

À l’ère de l’Intelligence Artificielle générative et des réseaux de neurones profonds, pourquoi revenir à un algorithme de 1960 ? La réponse réside dans l’efficacité et l’explicabilité.

• Données nécessaires : Les réseaux de neurones nécessitent des téraoctets de données historiques pour l’entraînement. Le filtre de Kalman ne nécessite que l’état précédent et la mesure actuelle. Il est opérationnel dès le « Jour 1 ».
• Coût Computationnel : Le filtre de Kalman est constitué de simples opérations matricielles. Il peut tourner sur des microcontrôleurs ou des serveurs surchargés avec une latence négligeable.
• Transparence : Si le modèle se trompe, nous pouvons inspecter la matrice $P$ ou le gain $K$ pour comprendre exactement pourquoi. Ce n’est pas une « Boîte Noire ».

Conclusions

Appliquer le filtre de Kalman en dehors de l’ingénierie électronique nécessite un changement de paradigme : il faut arrêter de voir les données business comme de simples nombres et commencer à les voir comme des signaux émis par un système dynamique. Qu’il s’agisse de prévoir la trajectoire d’un missile ou la propension à l’achat d’un client, les mathématiques de l’estimation d’état restent les mêmes. Pour les entreprises qui cherchent des avantages concurrentiels en temps réel, la maîtrise de ces outils de contrôle offre un avantage stratégique net par rapport aux concurrents qui s’appuient encore sur des moyennes statiques ou des modèles ML opaques et lents.

Foire aux questions

Sources et Approfondissements

1. Définition mathématique et historique du Filtre de Kalman (Wikipedia)
2. Rapport technique de la NASA sur l’utilisation du filtre de Kalman
3. Application financière : Estimation des taux d’intérêt et tendances (Federal Reserve)

Francesco Zinghinì

Ingénieur électronique avec pour mission de simplifier le numérique. Grâce à son bagage technique en théorie des systèmes, il analyse logiciels, matériel et infrastructures réseau pour offrir des guides pratiques sur l’informatique et les télécommunications. Il transforme la complexité technologique en solutions accessibles à tous.

LinkedInFacebookBiographie complète →