Em Resumo (TL;DR)
A abordagem de engenharia transforma os KPIs em sinais a processar, permitindo separar nitidamente as informações estratégicas do ruído de fundo dos dados.
A análise no domínio da frequência com a Transformada de Fourier revela ciclicidades invisíveis, superando as intuições baseadas na simples observação temporal.
Implementar o filtro de Kalman oferece uma estimativa da tendência em tempo real, eliminando o atraso de decisão causado pelas médias móveis clássicas.
O diabo está nos detalhes. 👇 Continue lendo para descobrir os passos críticos e as dicas práticas para não errar.
No panorama da Business Intelligence moderna, a análise de séries temporais representa frequentemente a fronteira entre uma decisão baseada na intuição e uma fundada na ciência de dados. No entanto, a maioria dos analistas limita-se a observar médias móveis e variações percentuais, ignorando um património metodológico que a engenharia eletrónica aperfeiçoou nas últimas décadas: o Signal Processing (Processamento Digital de Sinal).
Neste guia técnico, abandonaremos a abordagem estatística clássica para adotar uma visão de engenharia. Trataremos os KPIs empresariais (como o volume de pedidos de crédito habitação numa Fintech ou o cash flow diário) não como simples números numa folha de cálculo, mas como sinais elétricos afetados por ruído. Aplicando transformadas matemáticas e filtros digitais, aprenderemos a extrair a “tendência pura” (o sinal) das flutuações aleatórias do mercado (o ruído).

1. O Mindset de Engenharia: Sinal vs Ruído
Em eletrónica, um sinal recebido por um sensor está sempre contaminado por perturbações externas. O mesmo acontece nos dados empresariais. Se observarmos o gráfico das vendas diárias, vemos picos e vales. A questão fundamental é: aquela queda de terça-feira é uma tendência preocupante (Sinal) ou apenas uma variação aleatória devido à meteorologia ou a um feriado (Ruído)?
Para responder, devemos definir a relação Sinal/Ruído (SNR – Signal-to-Noise Ratio). Uma abordagem baseada na física dos sistemas ensina-nos que:
- O Sinal é a informação determinística, frequentemente de baixa frequência (tendência de crescimento) ou com frequência específica (sazonalidade).
- O Ruído é estocástico, frequentemente de alta frequência e distribuído aleatoriamente (ruído branco gaussiano).
2. Ferramentas e Pré-requisitos
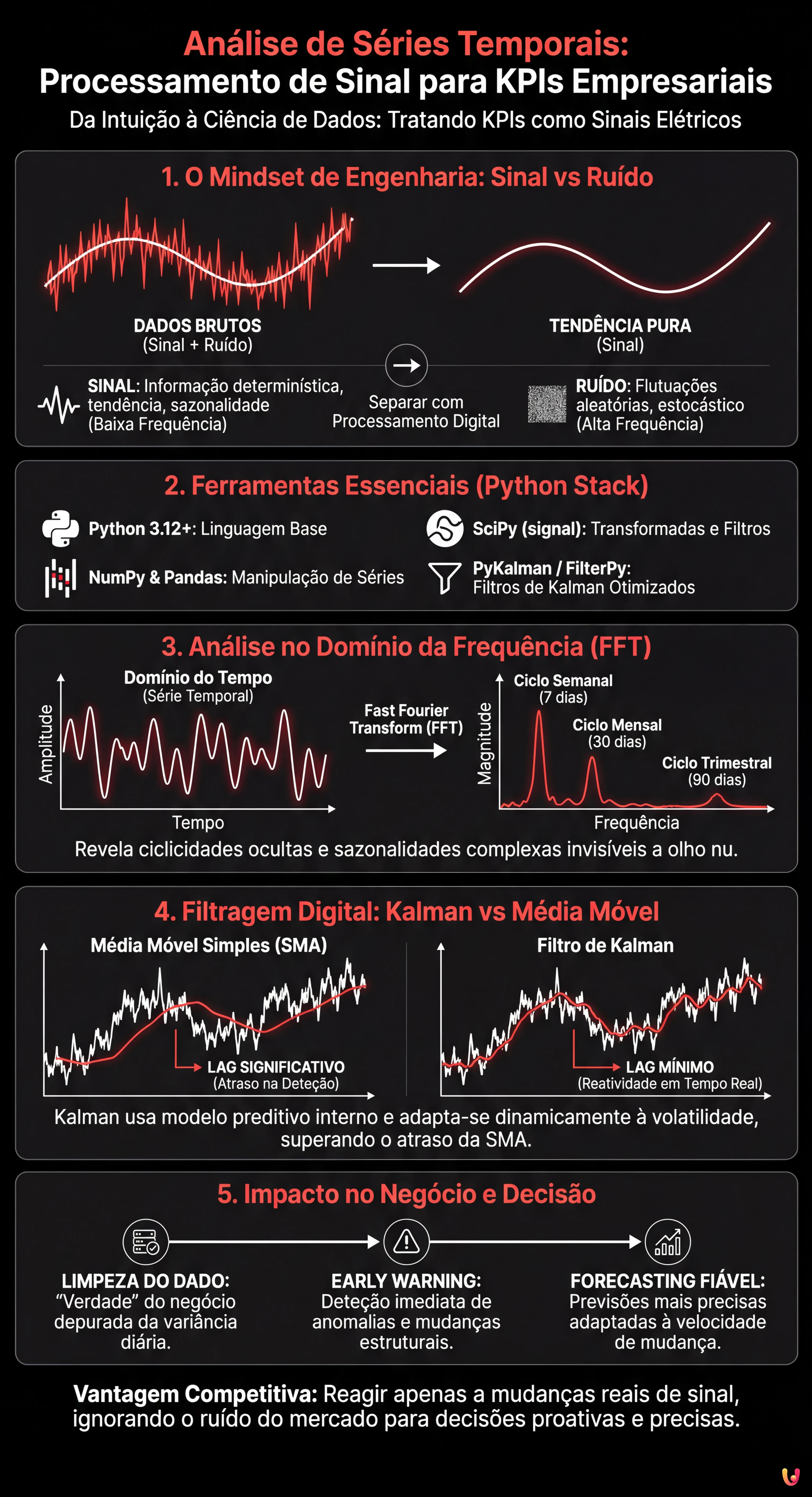
Para seguir este guia, não usaremos o Excel. A análise avançada de sinais requer potência de cálculo e bibliotecas específicas. Em 2026, a stack padrão para este tipo de operação inclui:
- Python 3.12+: A linguagem de referência.
- NumPy & Pandas: Para a manipulação das séries temporais.
- SciPy (módulo signal): Para a implementação de filtros digitais e transformadas.
- PyKalman ou FilterPy: Bibliotecas otimizadas para a implementação dos filtros de Kalman.
3. Análise no Domínio da Frequência: A Transformada de Fourier (FFT)

Um dos erros mais comuns na análise de séries temporais financeiras é tentar intuir a sazonalidade olhando para o gráfico no domínio do tempo. Um engenheiro eletrónico, por outro lado, desloca o problema para o domínio da frequência.
Utilizando a Fast Fourier Transform (FFT), podemos decompor o nosso KPI (ex. pedidos de crédito diários) nos seus componentes sinusoidais constitutivos. Isto permite-nos identificar ciclicidades ocultas que o olho humano não vê.
Aplicação Prática: Detetar a Ciclicidade do Crédito
Imaginemos que temos um dataset de 365 dias de pedidos. Aplicando a FFT, poderíamos ver um pico de magnitude na frequência correspondente a 7 dias (ciclo semanal) e um a 30 dias (ciclo mensal). Se notarmos um pico inesperado aos 90 dias, descobrimos uma ciclicidade trimestral ligada, por exemplo, a prazos fiscais, sem ter de a adivinhar.
4. Filtragem Digital: Além da Média Móvel
Uma vez compreendido o espectro do nosso sinal, devemos limpá-lo. A técnica mais usada no mundo empresarial é a Média Móvel Simples (SMA). Em engenharia, a SMA é considerada um filtro passa-baixo muito rudimentar com péssimas características de fase (introduz um atraso, ou lag, significativo).
O Problema do Lag
Se usar uma média móvel de 30 dias para prever o cash flow, o seu indicador dir-lhe-á que a tendência mudou com 15 dias de atraso. Num mercado volátil como o Fintech, este atraso é inaceitável.
A Solução: O Filtro de Kalman
O Filtro de Kalman é o algoritmo definitivo para a estimativa de estado em sistemas dinâmicos (usado desde o GPS aos sistemas de guiamento de mísseis). Ao contrário das médias móveis, o filtro de Kalman não se limita a “suavizar” o passado, mas:
- Possui um modelo interno da física do sistema (ex. a tendência de crescimento prevista).
- Compara a previsão do modelo com a nova medição real (o dado de hoje).
- Calcula o Ganho de Kalman: decide quanto confiar no modelo e quanto confiar na nova medição baseando-se na incerteza (covariância) de ambos.
O resultado é uma estimativa da tendência extremamente reativa que separa o ruído do sinal real quase em tempo real, reduzindo drasticamente o lag.
5. Caso de Estudo: Implementação em Python
Vejamos como aplicar estes conceitos a um dataset fictício de pedidos de empréstimo diários.
Passo 1: Análise Espetral com FFT
import numpy as np
import pandas as pd
from scipy.fft import fft, fftfreq
import matplotlib.pyplot as plt
# Carregamento de dados (Série temporal)
data = pd.read_csv('pedidos_credito.csv')
segnale = data['pedidos'].values
# Cálculo FFT
N = len(segnale)
T = 1.0 / 365.0 # Amostragem diária
yf = fft(segnale)
xf = fftfreq(N, T)[:N//2]
# Plot do espectro
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.title('Espectro de Frequências (Ciclicidade)')
plt.grid()
plt.show()Interpretação: Os picos no gráfico indicam os ciclos naturais do negócio. Se eliminarmos estas frequências (filtro notch), obtemos a tendência dessazonalizada de forma matematicamente rigorosa.
Passo 2: Smoothing com Filtro de Kalman
Para limpar o sinal mantendo a reatividade, usamos uma implementação base de um filtro de Kalman unidimensional.
from pykalman import KalmanFilter
# Configuração do Filtro
# transition_covariance: quão rapidamente muda a tendência real
# observation_covariance: quanto ruído existe nos dados diários
kf = KalmanFilter(transition_matrices=[1],
observation_matrices=[1],
initial_state_mean=segnale[0],
initial_state_covariance=1,
observation_covariance=10,
transition_covariance=0.1)
# Cálculo do sinal filtrado
state_means, _ = kf.filter(segnale)
# Comparação
data['Kalman_Signal'] = state_means
data[['pedidos', 'Kalman_Signal']].plot()
plt.title('Dados Brutos vs Filtro de Kalman')
plt.show()6. Interpretação dos Resultados para o Negócio
A aplicação destas técnicas de análise de séries temporais transforma o processo de decisão:
- Limpeza do Dado: A linha gerada pelo filtro de Kalman (
state_means) representa a “verdade” do negócio, depurada da variância diária aleatória. - Early Warning: Se o dado real se desvia do filtro de Kalman além de um certo limiar (ex. 3 desvios padrão da covariância residual), não é ruído: é uma anomalia ou uma mudança estrutural de mercado que requer intervenção imediata.
- Forecasting: Projetando o estado do filtro de Kalman no futuro, obtemos previsões de cash flow muito mais fiáveis em comparação com a regressão linear, porque o filtro adapta-se dinamicamente à velocidade de mudança do sistema.
Conclusões

Tratar os dados de negócio como sinais elétricos não é apenas um exercício académico, mas uma vantagem competitiva. Enquanto os concorrentes reagem ao ruído (ex. um dia de vendas fracas devido ao acaso), a empresa que utiliza o Signal Processing mantém o rumo, reagindo apenas quando o sinal indica uma real mudança estrutural. O uso da Transformada de Fourier e do Filtro de Kalman eleva a análise das séries temporais de simples observação a instrumento preditivo de alta precisão.
Perguntas frequentes

O Signal Processing aplicado aos KPIs é uma abordagem de engenharia que trata os dados de negócio, como as vendas ou o cash flow, não como simples números estatísticos, mas como sinais elétricos. Esta metodologia utiliza transformadas matemáticas e filtros digitais para separar a tendência real, definida como sinal, das flutuações aleatórias do mercado, identificadas como ruído. O objetivo é obter uma visão mais clara e científica do andamento empresarial, depurada das distorções momentâneas.
Na análise das séries temporais, o Sinal representa a informação determinística e valiosa, como uma tendência de crescimento estrutural ou uma sazonalidade recorrente de baixa frequência. O Ruído, pelo contrário, é constituído por variações estocásticas e aleatórias, frequentemente de alta frequência, devidas a fatores externos imprevisíveis como a meteorologia ou eventos isolados. Distinguir corretamente a relação Sinal Ruído permite evitar decisões baseadas em falsos alarmes.
O Filtro de Kalman é preferível à Média Móvel Simples porque resolve o problema do atraso, conhecido como «lag», típico dos indicadores clássicos. Enquanto a média móvel reage lentamente às mudanças suavizando apenas os dados passados, o filtro de Kalman combina um modelo preditivo interno com as medições em tempo real. Isto permite estimar a tendência atual com extrema reatividade e precisão, adaptando-se dinamicamente à volatilidade do sistema.
A Fast Fourier Transform, ou FFT, é fundamental para analisar os dados no domínio da frequência em vez do domínio do tempo. Esta ferramenta decompõe a série temporal nos seus componentes sinusoidais, permitindo identificar ciclicidades ocultas e sazonalidades complexas, como ciclos semanais ou trimestrais, que não seriam visíveis observando simplesmente o gráfico do andamento temporal dos dados.
Para implementar técnicas de Signal Processing nos dados empresariais, a stack tecnológica padrão baseada em Python inclui diversas bibliotecas especializadas. NumPy e Pandas são essenciais para a manipulação das séries temporais, enquanto o SciPy, em particular o módulo signal, é necessário para calcular transformadas e filtros. Para a implementação específica dos filtros preditivos, utilizam-se bibliotecas otimizadas como PyKalman ou FilterPy.



Achou este artigo útil? Há outro assunto que gostaria de me ver abordar?
Escreva nos comentários aqui em baixo! Inspiro-me diretamente nas vossas sugestões.