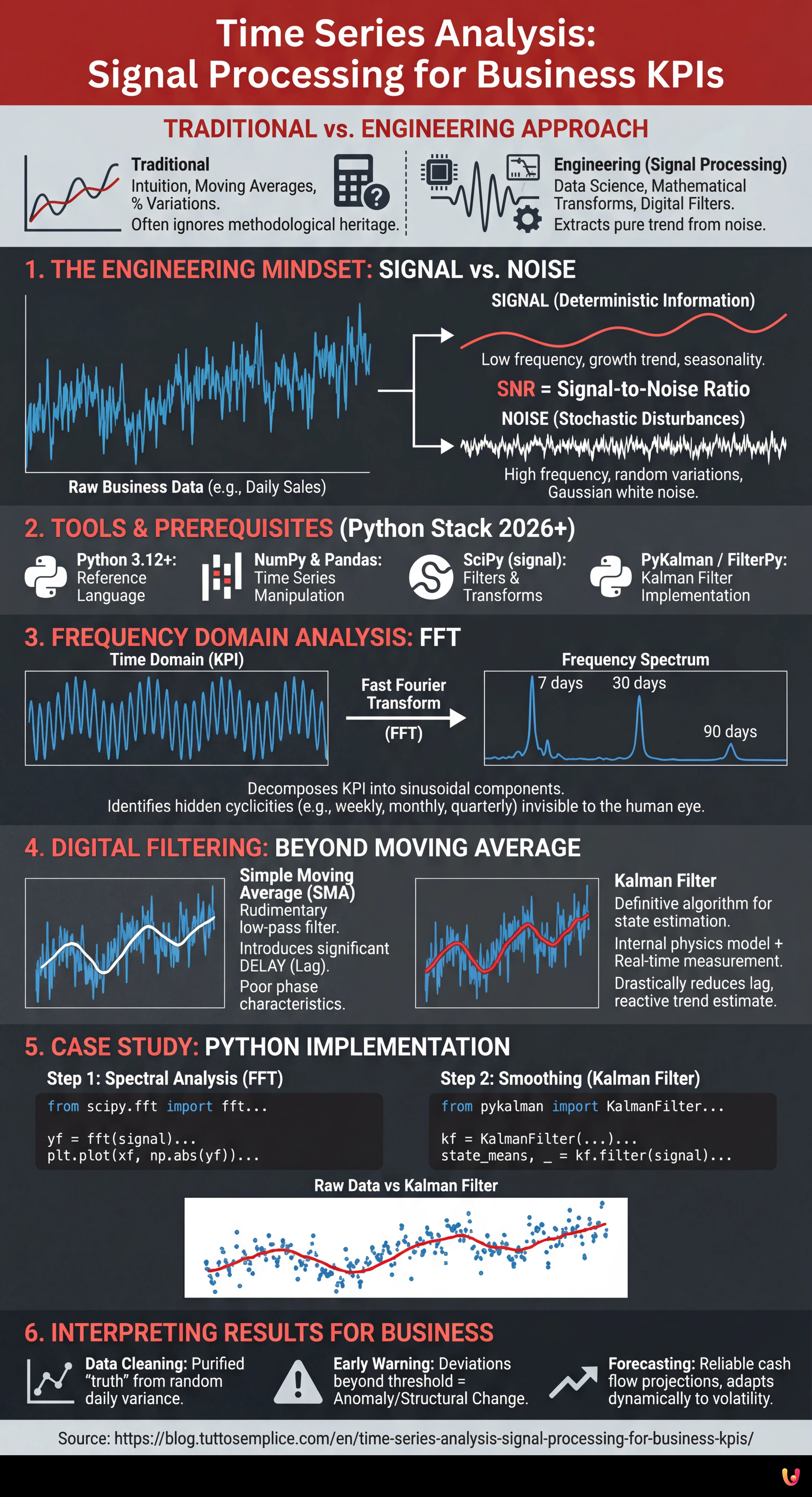
In Brief (TL;DR)
The engineering approach transforms KPIs into signals to be processed, allowing a clear separation of strategic information from data background noise.
Frequency domain analysis with the Fourier Transform reveals invisible cyclicities, surpassing intuitions based on simple temporal observation.
Implementing the Kalman filter offers real-time trend estimation, eliminating the decision-making lag caused by classic moving averages.
The devil is in the details. 👇 Keep reading to discover the critical steps and practical tips to avoid mistakes.
In the landscape of modern Business Intelligence, time series analysis often represents the boundary between a decision based on intuition and one founded on data science. However, most analysts limit themselves to observing moving averages and percentage variations, ignoring a methodological heritage that electronic engineering has perfected over the last few decades: Signal Processing (Digital Signal Processing).
In this technical guide, we will abandon the classic statistical approach to adopt an engineering vision. We will treat business KPIs (such as the volume of mortgage requests in a Fintech or daily cash flow) not as simple numbers on a spreadsheet, but as electrical signals affected by noise. By applying mathematical transforms and digital filters, we will learn to extract the “pure trend” (the signal) from random market fluctuations (the noise).

1. The Engineering Mindset: Signal vs Noise
In electronics, a signal received by a sensor is always contaminated by external disturbances. The same happens in business data. If we look at the graph of daily sales, we see peaks and valleys. The fundamental question is: is that dip on Tuesday a worrying trend (Signal) or just a random variation due to weather or a public holiday (Noise)?
To answer, we must define the SNR – Signal-to-Noise Ratio. An approach based on system physics teaches us that:
- The Signal is deterministic information, often low frequency (growth trend) or with specific frequency (seasonality).
- The Noise is stochastic, often high frequency and randomly distributed (Gaussian white noise).
2. Tools and Prerequisites
To follow this guide, we will not use Excel. Advanced signal analysis requires computing power and specific libraries. As of 2026, the standard stack for this type of operation includes:
- Python 3.12+: The reference language.
- NumPy & Pandas: For time series manipulation.
- SciPy (module signal): For implementing digital filters and transforms.
- PyKalman or FilterPy: Libraries optimized for Kalman filter implementation.
3. Frequency Domain Analysis: The Fourier Transform (FFT)

One of the most common mistakes in financial time series analysis is trying to intuit seasonality by looking at the graph in the time domain. An electronic engineer, however, moves the problem into the frequency domain.
Using the Fast Fourier Transform (FFT), we can decompose our KPI (e.g., daily mortgage requests) into its constituent sinusoidal components. This allows us to identify hidden cyclicities that the human eye cannot see.
Practical Application: Detecting Mortgage Cyclicity
Imagine having a dataset of 365 days of requests. By applying the FFT, we might see a magnitude peak at the frequency corresponding to 7 days (weekly cycle) and one at 30 days (monthly cycle). If we notice an unexpected peak at 90 days, we have discovered a quarterly cyclicity linked, for example, to tax deadlines, without having to guess it.
4. Digital Filtering: Beyond the Moving Average
Once we understand the spectrum of our signal, we must clean it. The technique most used in business is the Simple Moving Average (SMA). In engineering, the SMA is considered a very rudimentary low-pass filter with poor phase characteristics (it introduces significant delay, or lag).
The Lag Problem
If you use a 30-day moving average to forecast cash flow, your indicator will tell you that the trend changed with a 15-day delay. In a volatile market like Fintech, this delay is unacceptable.
The Solution: The Kalman Filter
The Kalman Filter is the definitive algorithm for state estimation in dynamic systems (used from GPS to missile guidance systems). Unlike moving averages, the Kalman filter does not limit itself to “smoothing” the past, but:
- Possesses an internal model of the system physics (e.g., the expected growth trend).
- Compares the model prediction with the new real measurement (today’s data).
- Calculates the Kalman Gain: decides how much to trust the model and how much to trust the new measurement based on the uncertainty (covariance) of both.
The result is an extremely reactive trend estimate that separates noise from the real signal almost in real-time, drastically reducing lag.
5. Case Study: Implementation in Python
Let’s see how to apply these concepts to a fictitious dataset of daily loan requests.
Step 1: Spectral Analysis with FFT
import numpy as np
import pandas as pd
from scipy.fft import fft, fftfreq
import matplotlib.pyplot as plt
# Load data (Time Series)
data = pd.read_csv('mortgage_requests.csv')
signal = data['requests'].values
# Calculate FFT
N = len(signal)
T = 1.0 / 365.0 # Daily sampling
yf = fft(signal)
xf = fftfreq(N, T)[:N//2]
# Plot spectrum
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.title('Frequency Spectrum (Cyclicity)')
plt.grid()
plt.show()Interpretation: The peaks in the graph indicate the natural cycles of the business. If we eliminate these frequencies (notch filter), we obtain the seasonally adjusted trend in a mathematically rigorous way.
Step 2: Smoothing with Kalman Filter
To clean the signal while maintaining reactivity, we use a basic implementation of a one-dimensional Kalman filter.
from pykalman import KalmanFilter
# Filter Configuration
# transition_covariance: how fast the real trend changes
# observation_covariance: how much noise is in the daily data
kf = KalmanFilter(transition_matrices=[1],
observation_matrices=[1],
initial_state_mean=signal[0],
initial_state_covariance=1,
observation_covariance=10,
transition_covariance=0.1)
# Calculate filtered signal
state_means, _ = kf.filter(signal)
# Comparison
data['Kalman_Signal'] = state_means
data[['requests', 'Kalman_Signal']].plot()
plt.title('Raw Data vs Kalman Filter')
plt.show()6. Interpreting Results for Business
Applying these time series analysis techniques transforms the decision-making process:
- Data Cleaning: The line generated by the Kalman filter (
state_means) represents the business “truth”, purified from random daily variance. - Early Warning: If the real data deviates from the Kalman filter beyond a certain threshold (e.g., 3 standard deviations of the residual covariance), it is not noise: it is an anomaly or a structural market change requiring immediate intervention.
- Forecasting: By projecting the Kalman filter state into the future, we obtain cash flow forecasts that are much more reliable than linear regression, because the filter adapts dynamically to the speed of system change.
Conclusions

Treating business data as electrical signals is not just an academic exercise, but a competitive advantage. While competitors react to noise (e.g., a day of poor sales due to chance), the company using Signal Processing stays the course, reacting only when the signal indicates a real structural change. The use of the Fourier Transform and the Kalman Filter elevates time series analysis from simple observation to a high-precision predictive tool.
Frequently Asked Questions

Signal Processing applied to KPIs is an engineering approach that treats business data, such as sales or cash flow, not as simple statistical numbers but as electrical signals. This methodology uses mathematical transforms and digital filters to separate the real trend, defined as signal, from random market fluctuations, identified as noise. The goal is to obtain a clearer and more scientific view of business performance, purified from momentary distortions.
In time series analysis, the Signal represents deterministic and valuable information, such as a structural growth trend or recurring low-frequency seasonality. Noise, on the contrary, consists of stochastic and random variations, often at high frequency, due to unpredictable external factors like weather or isolated events. Correctly distinguishing the Signal-to-Noise ratio allows avoiding decisions based on false alarms.
The Kalman Filter is preferable to the Simple Moving Average because it solves the delay problem, known as lag, typical of classic indicators. While the moving average reacts slowly to changes by smoothing only past data, the Kalman filter combines an internal predictive model with real-time measurements. This allows estimating the current trend with extreme reactivity and precision, adapting dynamically to system volatility.
The Fast Fourier Transform, or FFT, is fundamental for analyzing data in the frequency domain rather than the time domain. This tool decomposes the time series into its sinusoidal components, allowing the identification of hidden cyclicities and complex seasonalities, such as weekly or quarterly cycles, which would not be visible by simply observing the graph of the temporal data trend.
To implement Signal Processing techniques on business data, the standard technology stack based on Python includes several specialized libraries. NumPy and Pandas are essential for time series manipulation, while SciPy, specifically the signal module, is necessary for calculating transforms and filters. For the specific implementation of predictive filters, optimized libraries like PyKalman or FilterPy are used.



Did you find this article helpful? Is there another topic you'd like to see me cover?
Write it in the comments below! I take inspiration directly from your suggestions.